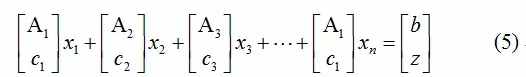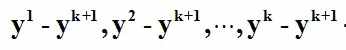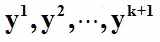运筹学单纯形法（单纯形法各个步骤详解）

R帷幄』原创

作者：臧永森

作者：臧永森，清华大学工业工程系在读博士，研究方向：运筹优化算法的设计与应用、数据统计分析、大数据技术与应用，戚铭尧老师团队

编者按

此文属于电子书线性规划专题第三章单纯形法的内容。在前面的文章中，我们为引入单纯形法介绍了可行域、最优解、可行解、基解、基可行解等基础概念，也阐述了它们之间的关系（具体可见文章《在单纯形法之前》）。在明确了这些基本概念之后，这一节我们来探讨单纯形法的思想逻辑和求解步骤。

我们已经知道，优化问题的最优解一定是基可行解，那么如何找到最优的基可行解就是最优化问题的求解思路。因此，单纯形法在求解过程，就是不断地寻求变量出入基的循环迭代过程，每次迭代都达到降低目标函数值（或增大目标函数值）的目的，最终得到最优解。那么在迭代过程中，如何使解在改善过程中向着最优解的方向尽快地收敛呢？我们下面用比较直观的方式来解析这个过程。

单纯形法的基本思想与逻辑

本文采用的思路参考Dimitris Bertsimas和 John N. Tsitsiklis在 Introduction to Linear Optimization一书中提出的方法[1]。考虑如下标准线性规划问题：

我们将矩阵A拆分为n个列元素：A1, A2, A3,, An，那么我们可以将问题看成是满足非负约束（4）、凸约束（3）以及约束（5）的最小化问题。

结合式（3）和（5）我们可以看出，原优化问题转化为求解能够构造出（b, z）的使得z值最小的关于（Ai, ci）的凸组合。为了更好地理解它们之间的几何关系，我们将一个平面视作*含A的一个m维空间，将与ci相关的成本项看作是一维垂直数轴，这时每一个点（Ai, ci）都可以唯一在该三维坐标系中表示出来，如图1所示：

图1 线性规划问题1—4的“列几何”图示

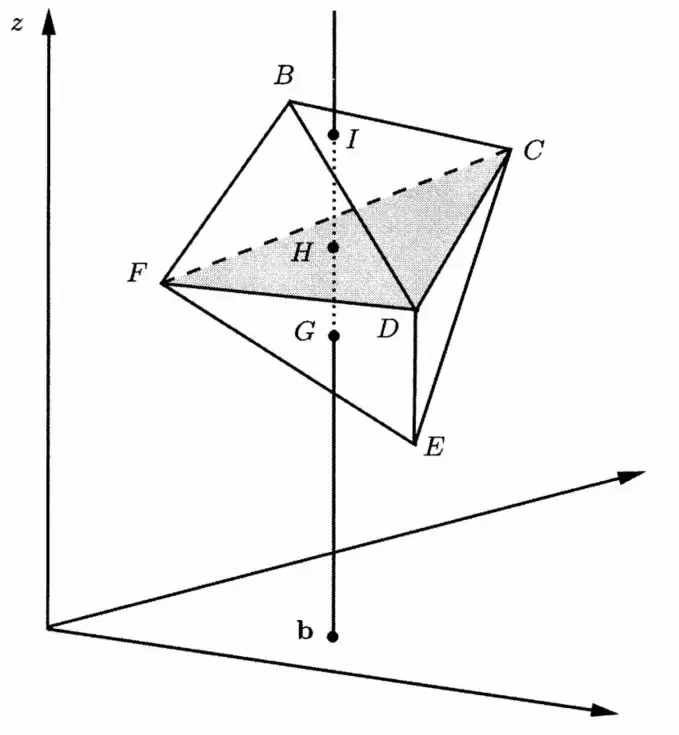
我们将（b, z）同样视为一条垂直线表示在图1中，这条垂直线叫做需求线，其与平面的交点是（b, 0）点。需求线与（Ai, ci）的凸组合在几何上有一定的关系，它们或相交或相离，这取决于我们对（Ai, ci）凸组合的选取，选取的凸组合不一样，几何关系就不同。很容易能理解，如果需求线和凸组合相交，说明（b, z）可以用相应的凸组合表示出来，也就表明这个凸组合就是原问题的一个可行解；而如果相离，则说明这个凸组合不满足能够表达（b, z）的条件，也就不是原问题的可行解。所有的凸组合构成了一个凸*，如果需求线能够与凸*相交，那么原问题就存在可行解，如果需求线不能与凸*相交，说明原问题无解。进一步将图1抽象，得到图2，从图中我们可以看出，点I、H、G就是三个不同的凸组合与需求线的交点，也就是原问题的三个可行解。

图2 可行解的“列几何”图示

经过上面的分析我们得知，要找到最优解，就是找到与需求线相交的使得z值最小的凸组合。那么如何找这样的凸组合呢？首先引入两个定义：

如果向量

是线性独立的，那么向量

被称为Rn空间中的仿射独立或者仿射无关，其中k<=n。
在Rn空间中由k+1个仿射无关向量组成的凸*被称为k维单纯形。

对模型（1—4）来说，总共有m+1个等式约束，假定约束系数矩阵是满秩的，那么一个基可行解将对应m+1个线性独立的列向量，也就意味着有m+1个基点，根据上述定义，由基点之间的差向量线性独立可以得到其仿射独立，由此可以知道它们组成的凸*是m维单纯形。

假设m维单纯形与需求线相交于点（b, z），由（5）知用来表示（b, z）的线性组合的权重向量是xi ，该向量就是一个基可行解，也就对应我们上节所分析的基变量的内容，当然z就是相应的目标函数值。我们用图2做一个解释，阴影区域的三角形CDF，就是一个2维单纯形，其与需求线的交点H点就是基可行解，点C、D、F是基点。

我们对二维单纯形CDF做一些改变，会发现相应的z值（与需求线的交点）也会变化，比如我们令基点B取代基点F，单纯形变为BCD，这时可行解变为I点，相应的z值较之前有所增长。类似地，若点E取代点C成为基点，单纯形由CDF变为EDF，可行解就出现在G点，此时z值有所减小。从这些变化中我们找出这样一个规律，当且仅当新加入基的点在当前单纯形平面上方（下方）时，所得的交点（即可行解）对应的z值会增大（减小）。

如果我们更加形象地描述这个基点变化的过程，就如同用手抓住单纯形CDF的基点C，保持D点和F点固定不变，用力向上拉（向下拉），将C点拉到B点（E点），也就产*了新的单纯形BCD（EDF）。单纯形法的旋转迭代过程，就是不断找到基点向上拉（向下拉）到新基点形成新单纯形的过程。

单纯形法的求解过程

简单总结一下单纯形法的求解原理。先找到一个基可行解，然后从非基解中找一个比较有前途的点入基，替换掉基可行解中有待改善的基点，从而达到改善目标函数的目的，如此重复迭代，直至无法找到可以入基的点。